Quickly Calculate Compound Interest 💵
On Lump Sum and/or Regular Deposits Into a High Yield Savings Account
Investing In Series I Savings Bonds
While the Federal Reserve has lifted interest rates aggressively in 2022 most commercial banks have been slow to follow suit, with many of them parking their depositor's money at the Fed as excessive reserves & earning the interest you could have earned directly.
U.S. citizens & green card holders can invest in up to $10,000 worth of I bonds per year on TreasuryDirect. Each EIN can purchase up to $10,000 per year. Parents who have purchased the limit can also create minor-linked accounts to purchase bonds for young children, or purchase bonds for adult children. Each person which onws I bonds is required to have a TreasuryDirect account.
Interest is paid semi-annually & any I bonds bought through October 2022 I bonds pay an APR of 9.62% for the first 6 months. The rate of interest is adjusted twice per year based on the CPI-U.
The interest income is not taxable at the State & local level, though is taxable at the Federal level. Using the interest income to fund higher education may allow you to be exempted from the Federal income tax on the interest.
How To Use This Tool
The Basics
Use this calculator to quickly figure out how much money you will have saved up during a set investment period. First, enter your initial amount you have set aside, then enter the interest rate along with how long you tend to invest for.
Next enter how much money you intend to deposit or withdrawal periodically. If this calculation is for a lump sum deposit with no recurring transactions enter "Never" in the "add money" drop down.
Once you have entered this information the calculator will inform you of how much money you will have saved up before income taxes, how much income tax you'll owe & what the remaining amount of money is worth in real terms after accounting for inflation.
Calculations update automatically when any input is changed. If you have a particular savings goal you want to reach by a specific date then please use our savings goal calculators.
If you would like to print out a schedule of your savings growth over time, please click on the "Create Growth Table" button to generate a printable schedule of your payment history, accumulated interest & balance.
Calculation Mechanics
How Interest is Compounded
Our calculator compounds interest each time money is added. If the account has a lump-sum initial deposit & does not have any periodic deposit, by default interest is compounded monthly. Most bank savings accounts use a daily average balance to compound interest daily and then add the amount to the account's balance monthly, which is mathematically quite similar to monthly compounding.
If you would like to change the compounding frequency for a one-time deposit then set the "deposit each cycle" variable to $0 and select "transaction frequency" at whatever frequency you wish to compound interest.
When Contributions Are Made
In the above calculator when recurring account contributions are made, money is added or subtracted at the beginning of each month, week, or other selected period. If you would like to end money at the end of each month then you would subtract the regular contribution amount from the initial savings to calculate interest at the end of the month.
How Income Taxes Are Accounted For
This calculator estimates taxes based on the rate entered with the tax payment made at the end of the investment period. This approach is how tax payments would work on savings stored inside a tax deferred retirement account.
Ordinary interest on a regular bank savings account is typically paid for on an annual basis, with banks sending account holders a 1099-INT if they earn above some baseline level of around $10. If your account is untaxed then enter zero as the marginal tax rate in the above calculator.
How Inflation is Accounted For
After taxes are deducted from interest earnings & final savings are calculated, inflation is accounted for by multiplying the final amount by (100% - inflation rate)years

How to Calculate Compound Interest
The easy way to do this is to use the above calculator. The hard way would be manually calculating the returns.
Single Deposit
The above calculator automatically does this for you, but if you wanted to calculate compound interest manually the formula is
FV = PV * (1 + r/n)nt
Formula definitions:
- FV = future value
- PV = present value (initial deposit)
- r = annual interest rate, as a decimal rather than percent (also called APR)
- n = number of times interest is compounded per year
- t = time in years
To find the interest which was earned from the account all you would need to do is subtract the initial deposit amount from the end result.
A Series of Deposits
End of the Month
For recurring monthly deposits where deposits are made at the end of each month you would use the following calculation.
FV = PMT * (((1 + r/n)nt - 1) / (r/n))
All the definitions in this formula are the same as the definitions in the first formula, except PMT is the monthly deposit.
If you want to figure out how much interest was earned then you would simply subtract the payment amount times how many payment cycles were made from the end total.
If you deposited $200 per month for 2 years you would then subtract the $2,400 in deposits from the total to get the interest earned.
Beginning of the Month
If the deposits occur at the beginning of each month you would use the same exact formula, but then add 1 more monthly calculation to it.
FV = PMT * (((1 + r/n)nt - 1) / (r/n)) * (1 + r/n)
Series of Deposits, With Initial Deposit
If you made a series of deposits and there was an initial lump sum deposit then you would treat the series and the initial deposit as two separate entities & then add each total together to get your final savings amount.
Taxes & Inflation
This would be the first step of calculating your returns, then you would need to subtract income taxes from the returns & then account for inflation.
Multiply your interest earned against income tax rate (as a decimal) and that will be the total amount of taxes paid. Subtract that amount from your future savings value to get your savings after taxes.
To account for inflation you would use the following formula
PV = FV * ( 1 - i)n
The present value of a future sum of money is equal to the future value times (1 - the annual rate of inflation as a decimal) raised to the nth power, where n is the number of years into the future.
How to Find Current Interest Rates
Tracker Sites Listing Today's Offered Savings Rates
A number of popular websites like Credit Karma, Nerd Wallet & BankRate track current rates on offer for various savings vehicles like high-yield savings accounts, CDs. and even life insurance products. Typically life insurance policies have fees for early withdrawal & many hidden fees embedded in them which make their returns lower than other options.
Some tracker sites appear neutral, but are paid a commission for listing select players across the market, so it can be beneficial to view the full set of listings from each comparison website to ensure you are seeing the highest rate rather than who was willing to pay the most for exposure. It is also worth taking the time to compare your options across multiple sites in case one of them was able to get an exclusive promotional offer.
Treasuries: The Benchmark
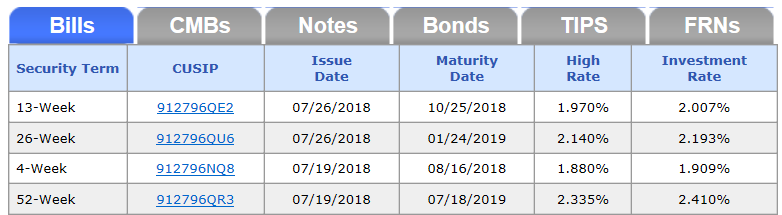
United States citizens can invest in Treasuries at TreasuryDirect. They also publish recent auction results for notes, bills & bonds of various durations.
Most corporate bonds typically trade at a higher yield than government bonds, as governments are guaranteed to be able to nominally repay their debts denominated in their own currency using currency they print.
The nominal interest earned may not keep up with inflation, especially after income taxes are deducted from earnings, which is part of the reason people who are not risk-adverse & do not need money in the short run are encouraged to invest in equities.
“Long term bonds are a terrible investment at current rates...T-bonds haven’t been attractive ever except in the early 1980s, when they briefly offered a 14% return.” - Warren Buffett, 2018
Duration Credit Risk
As a general rule of thumb, the longer a person is willing to lock up their capital the higher the rate they will be paid on deposits. For example, in most cases the rate on a 5-year CD is typically higher than the rate on a 1-year CD, which would be higher than the rate available on an ordinary savings or checking account.
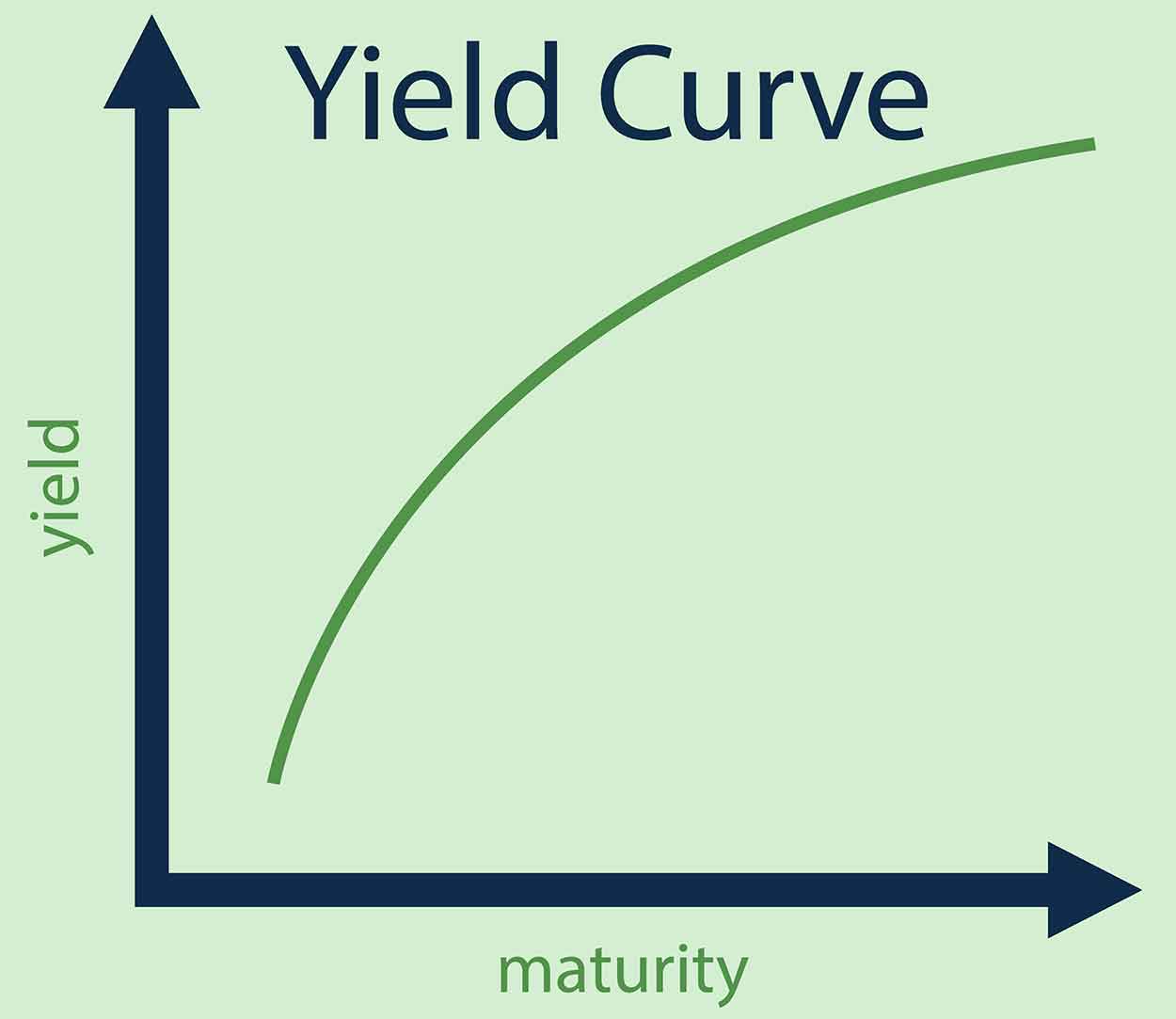
The Federal Reserve controls short-term interest rates to help achieve their dual mandate of stable prices and low unemployment levels. These rates in turn help drive creditor preferences across the economy. The level & the shape of the curve changes over time.

When the economy is growing smoothly the duration risk in credit products is reflected in an upward sloping yield curve on treasuries. When investors become less certain about the future economic landscape the yield curve can flatten or even invert. Typically when the yield curve inverts to where 2 year notes yield more than 10 year notes there is a recession in the subsequent 12 to 18 months.
If interest rates jump sharply while an investor has an investment in a long-duration debt instrument then the mark-to-market losses on such an investment can be substantial. If a person has 28 years remaining on a $10,000 30-year bond which pays 3.5% interest and interest rates jump to 6% then the imputed loss of interest income on that bond is 2.5% (the change in interes rate) times the size of the bond ($10,000) times the years remaining (28).
A person who holds the bond until duration will still receive their $10,000 principal & the remaining $9,800 in interest throughout the remainder of the term. But if they are forced to sell it today they are competing against other fresh/new bonds which offer the 6% interest rate. A 30-year bond yielding 6% would pay $16,800 over those same 28 years, along with another $1,200 in the subsequent 2 years.
Changing interest rates have a major impact on the imputed value of existing bonds, with prices & yields being inversely correlated. For a person to purchase an existing bond with a low yielding coupon instead of a new higher-yielding bond they require a discount. To match the same yield-to-maturity the formula is as follows.
YTM = (C + (F - P) / n) / (F + P) * 0.5
- YTM: approximate yield to maturity
- C: coupon / annual interest payment
- F: face value of the bond
- P: price of the bond
- n: years until maturity
If a new bond yields 6% then the old 3.5% bond's price would need to fall from $10,000 to $6,629.32 in order to have the same yield-to-maturity.
Mitigating Credit Risk
Investors who invest in open-end bond funds may have the value of their investment diminished if other co-investors in the same fund liquidate their holdings during market turbulence. When an open ended bond fund investor exits their position at distressed prices they lock in losses for other investors as the fund must sell some bond holdings at distressed prices to fund the withdrawal.
Close ended funds do not have the same co-investor risk as the open-ended funds since the fund price may change on exit but the core holdings do not change, meaning that one can wait out the duration and not eat a loss induced by other investors selling in a panic.
To mitigate credit risks some investors invest a portion of their funds into a bond ladder where they have a regularly scheduled set of bonds maturing each year or every few years.
What if Market Conditions Change?
An Example Change
If you anticipate market conditions changing drastically you can break your calculation into 2 stages. For example, "bond king" Jeffrey Gundlach stated in December 2017 he expected the United States 10-year Treasury yield would hit 6% by 2020.
Significantly higher bond rates would likely force banks to pay investors higher rates of interest to attract capital to high yield savings accounts or CD investments.
Two Options: Estimate Average or Run Multiple Calculations
You could either estimate the average interest rate you will receive during the duration of your investment or you could break your calculation down into 2 stages.
Breaking Down Calculation
run a calculation using current settings for 2 years,
use the output of the first calculation as the initial savings in a second calculation & run a second calculation with a higher rate of interest for subsequent years
Here is an example of the breaking down approach using the following criteria:
- initial savings = $10,000
- monthly deposit = $500
- overall investment term = 7 years
- initial interest rate for first 2 years = 1.7%
- interest rate for subsequent years = 4.5%
- income tax rate = 25%
- inflation rate = 2%
The first 2 years calculation results are as follows:
- Total amount deposited: $22,000
- Interest earned: $560.42
- Income tax: $140.11
- Savings after taxes: $22,420.32
- Purchasing power: $21,532.47
The next 5 years calculation starts with the $22,420.32 as the initial deposit then adjusts term to remaining 5 years at 4.5% interest.
- Interest earned (during 5-year period): $9,344.02
- Income tax (during 5-year period): $2,336.00
- Final savings after tax: $59,428.33
Averaging
The second option would be averaging the rates together to create a blended average rate.
- (1.7% * 2 years + 4.5% * 5 years) / 7 years =
- 3.4 + 22.5 / 7 =
- 25.9 / 7 = 2.8556%
Which Approach is Better?
Each of these strategies has strengths and weaknesses.
The strength of the second option is seeing estimated spending power of the set final number accounting for the compounded impacts of inflation throughout the entire investment period.
The strength of the first option is it is much quicker to do.
Markets Are Uncertain
With either approach you are only going to get a rough approximation of performance as market conditions are quite unpredictable. That is plenty good enough in most cases though, because nobody can consistently predict the markets.
- In 2007 almost nobody predicted the crisis of 2008. Fed Chairman Bernake claimed subprime was contained.
- In 2008 almost nobody thought "emergency" monetary policies would last a decade.
- In 2015 almost nobody (other than Scott Adams - the author of Dilbert) predicted the election of Donald Trump, which ushered in a large change to federal income taxes.
Irrational Herding Behavior
Even some of the greatest investors of all time tout how the irrationality of market behavior provides them greater returns.

Buffett in 1978:
"The stock-market is manic-depressant which is ideal. When the market moves up, institutions jump in in large numbers because they fear what their clients will say if they miss a major move. The fear of losing accounts is the driving force behind institutions. pic.twitter.com/CLxmOkKmeo
— La nuit sera calme (@NuitSeraCalme) May 10, 2018
Concentrated Bets
James Clear wrote"Your odds of success improve when you are forced to direct all of your energy and attention to fewer tasks." Warren Buffett advocates making fewer higher-confidence investments rather than spreading oneself too thin.
When Warren lectures at business schools, he says, “I could improve your ultimate financial welfare by giving you a ticket with only 20 slots in it so that you had 20 punches — representing all the investments that you got to make in a lifetime. And once you'd punched through the card, you couldn't make any more investments at all.”
He says, “Under those rules, you'd really think carefully about what you did and you'd be forced to load up on what you'd really thought about. So you'd do so much better.”
Investing in Compounding Knowledge
A great way to have a sustainable competitive advantage in the market is to learn uncommon knowledge that does not change.
"When you learn something that doesn’t change, you can step off the treadmill of keeping up and start to compound your knowledge. While this compounding may at first slow you down, it offers exponential returns. And what better investment can you make than learning, with deep fluency, timeless principles like second-order thinking, something that applies to a wide variety of situations and is likely to remain constant?"
This advice is echoed by Amazon.com founder Jeff Bezos:
"I very frequently get the question: 'What's going to change in the next 10 years?' And that is a very interesting question; it's a very common one. I almost never get the question: 'What's not going to change in the next 10 years?' And I submit to you that that second question is actually the more important of the two — because you can build a business strategy around the things that are stable in time. … [I]n our retail business, we know that customers want low prices, and I know that's going to be true 10 years from now. They want fast delivery; they want vast selection. It's impossible to imagine a future 10 years from now where a customer comes up and says, 'Jeff I love Amazon; I just wish the prices were a little higher,' [or] 'I love Amazon; I just wish you'd deliver a little more slowly.' Impossible. And so the effort we put into those things, spinning those things up, we know the energy we put into it today will still be paying off dividends for our customers 10 years from now. When you have something that you know is true, even over the long term, you can afford to put a lot of energy into it."
How Much Money Should You Save Each Month?
A good rule of thumb is to try to save 20% of your net (after-tax) income each month. As part of the 50/30/20 rule it states you should spend a maximum of 50% of your check on life's necessities, up to 30% on discretionary spending & save at least 20% of your paycheck.
In some cases the above may not be possible, however the faster your save the more flexibility & freedome you give yourself in life.
How you invest & what you invest in are as important as how much you save. Regularly trading in and out of positions can incur high tax costs. Many 401(k) and IRA accounts come with high management fees that far exceed the value of the investment management services. Low-cost index funds can give a person close to market returns without spending much on management fees.
Imagine you have $100,000 invested. If the account earned 6% a year for the next 25 years and had no costs or fees, you'd end up with about $430,000.
If, on the other hand, you paid 2% a year in costs, after 25 years you'd only have about $260,000.
That's right: The 2% you paid every year would wipe out almost 40% of your final account value. 2% doesn't sound so small anymore, does it?
Guides to Understanding the Capital Markets
- Burton G. Malkiel's A Random Walk Down Wall Street is a great book offering wisdom on how one can succeed in volatile markets.
- Bogleheads - community forum which advocates low-cost passive investing strategies pioneered by Vanguard founder John C. Bogle. Small annual fees can have a dramatic impact on compounded returns:
- The Reformed Broker - blog by financial advisor Joshua M. Brown.
- The Big Picture - blog by Barry Ritholtz covering the economy & effective investment strategies.
- Market Ticker - blog by Karl Denninger covering politics & the capital markets.
- Howard Lindzon - personal blog of the momentum trader & venture capitalist investor.
- TastyTrade - financial news network created by options trader Tom Sosnoff.


I very frequently get the question:
'What's going to change in the next 10 years?' And that is a very interesting question; it's a very common one. I almost never get the question: 'What's not going to change in the next 10 years?' And I submit to you that that second question is actually the more important of the two — because you can build a business strategy around the things that are stable in time. … [I]n our retail business, we know that customers want low prices, and I know that's going to be true 10 years from now. They want fast delivery; they want vast selection. It's impossible to imagine a future 10 years from now where a customer comes up and says, 'Jeff I love Amazon; I just wish the prices were a little higher,' [or] 'I love Amazon; I just wish you'd deliver a little more slowly.' Impossible. And so the effort we put into those things, spinning those things up, we know the energy we put into it today will still be paying off dividends for our customers 10 years from now. When you have something that you know is true, even over the long term, you can afford to put a lot of energy into it." - Jeff Bezos