Quickly Calculate Compound Interest on Lump Sum Deposits
Into High Yield Savings Accounts
How To Use This Tool
The Basics
Use this calculator to quickly figure out how much money you will have saved up during a set investment period. Enter your initial amount you have to invest, then enter the interest rate along with how long you tend to invest for. Next select how frequently you want interest to compound. By default interest is compounded continuously on this calculator, though you can select other options including: daily, weekly, biweekly, semi-monthly, monthly, bimonthly, quarterly, semi-annually or yearly.
Most banks compute savings account interest based on the daily average balance of the account & add interest to the account at the end of each month. If you would like to calculate interest similarly to how banks do, then it would be best to select monthly compounding.
Once you have entered this information the calculator will inform you of how much interest you will have earned, how much money you will have saved up before income taxes, how much income tax you'll owe & what the remaining amount of money is worth in real terms after accounting for inflation.
Calculations update automatically when any input is changed. If you have a particular savings goal you want to reach by a specific date then please use our savings goal calculators. If you are making ongoing deposits please use the calculator on our homepage.
If you would like to print out a schedule of your savings growth over time, please click on the "Create Growth Table" button to generate a printable schedule of your payment history, accumulated interest & balance. This feature shows the compounded interest earned over each interval. If you select "Continuous" compounded interest it will generate a table which shows the accumulated interest after each year in the printable results.
Calculation Mechanics
How Interest is Compounded
Our calculator compounds interest at whatever periodicity the user selects. Most bank savings accounts use a daily average balance to compound interest daily and then add the amount to the account's balance monthly, which is mathematically quite similar to monthly compounding.
When Contributions Are Made
In the above calculator when recurring account contributions are made, money is added or subtracted at the beginning of each month, week, or other selected period. If you would like to end money at the end of each month then you would subtract the regular contribution amount from the initial savings to calculate interest at the end of the month.
How Income Taxes Are Accounted For
This calculator estimates taxes based on the rate entered with the tax payment made at the end of the investment period. This approach is how tax payments would work on savings stored inside a tax deferred retirement account.
Ordinary interest on a regular bank savings account is typically paid for on an annual basis, with banks sending account holders a 1099-INT if they earn above some baseline level of around $10. If your account is untaxed then enter zero as the marginal tax rate in the above calculator.
How Inflation is Accounted For
After taxes are deducted from interest earnings & final savings are calculated, inflation is accounted for by multiplying the final amount by (100% - inflation rate)years
How to Calculate Compound Interest
The easy way to do this is to use the above calculator. The hard way would be manually calculating the returns. The above calculator automatically does this for you, but if you wanted to calculate compound interest manually the formula is
FV = PV * (1 + r/n) n t
Formula definitions:
- FV = future value
- PV = present value (initial deposit)
- r = annual interest rate, as a decimal rather than percent (also called APR)
- n = number of times interest is compounded per year
- t = time in years
To find the interest which was earned from the account all you would need to do is subtract the initial deposit amount from the end result.
The formula for continuously compounded interest is similar to the above, except the rate of interest is moved into the exponent part of the calculation & the mathematical constant e is used.
FV = PV * (e) r t
e is also known as Euler's number. It is a famous irrational number named after Swiss mathematician Leonhard Euler which begins with 2.71828 & has a natural logarithm of 1. Here is Euler's formula
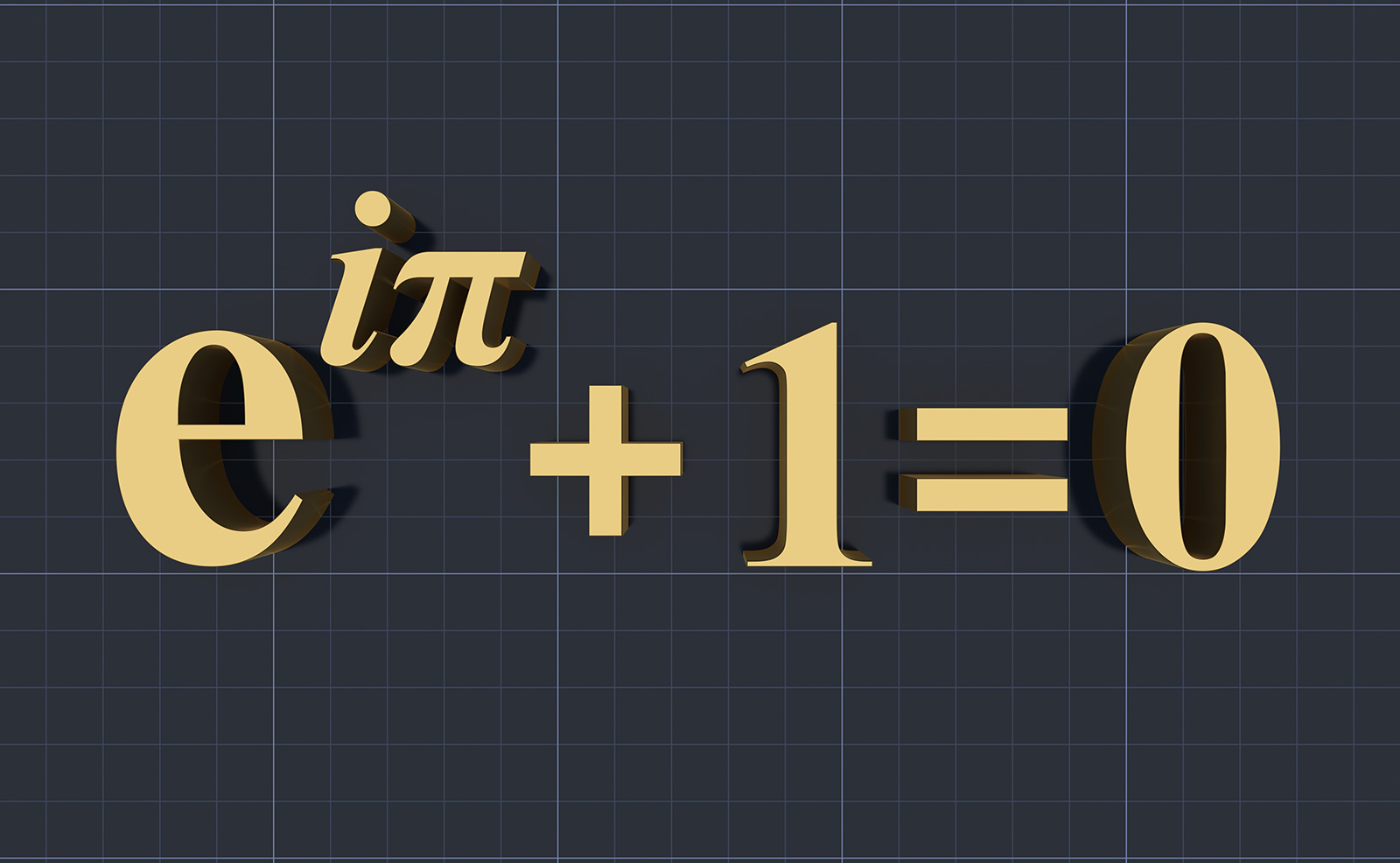


I very frequently get the question:
'What's going to change in the next 10 years?' And that is a very interesting question; it's a very common one. I almost never get the question: 'What's not going to change in the next 10 years?' And I submit to you that that second question is actually the more important of the two — because you can build a business strategy around the things that are stable in time. … [I]n our retail business, we know that customers want low prices, and I know that's going to be true 10 years from now. They want fast delivery; they want vast selection. It's impossible to imagine a future 10 years from now where a customer comes up and says, 'Jeff I love Amazon; I just wish the prices were a little higher,' [or] 'I love Amazon; I just wish you'd deliver a little more slowly.' Impossible. And so the effort we put into those things, spinning those things up, we know the energy we put into it today will still be paying off dividends for our customers 10 years from now. When you have something that you know is true, even over the long term, you can afford to put a lot of energy into it." - Jeff Bezos

